Tempo di lettura/visione: 3 min
Tempo di lettura/visione: 3 min
 Consigliato per la fascia d'età: PRIMARIA
Consigliato per la fascia d'età: PRIMARIA
Introduzione
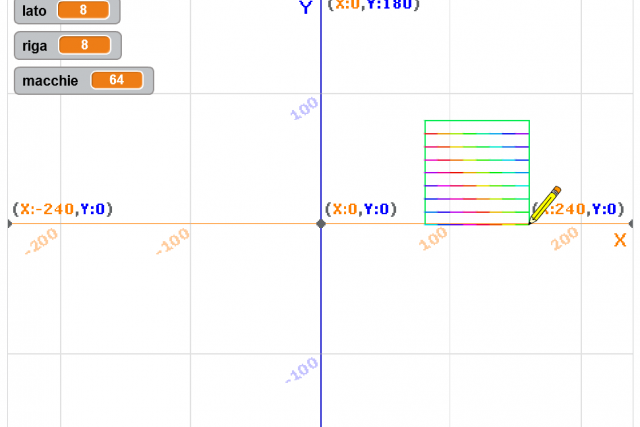
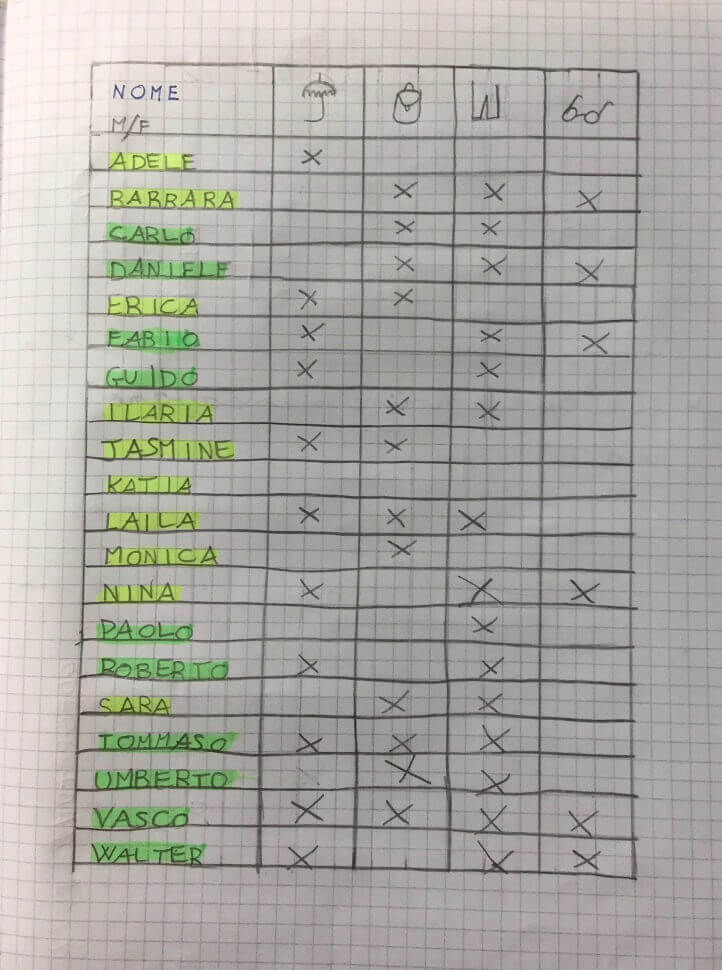
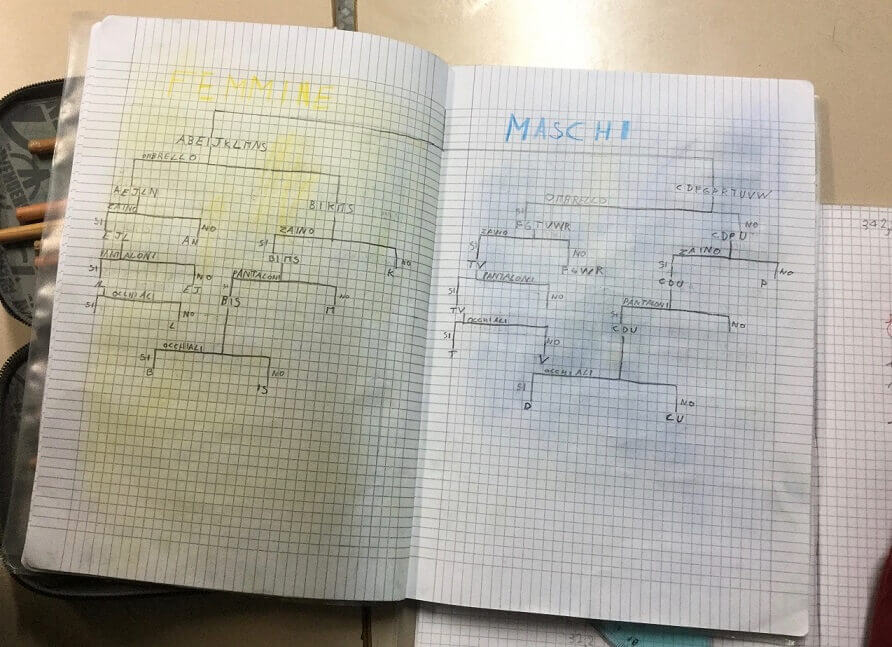
Percorso di logica dalle tabelle alle schede perforate
Con il termine logica, dal greco λόγος, logos, ovvero "parola", “pensiero”, "ragione" (crf. P. Odifreddi), si intende la capacità di eseguire ragionamenti corretti e di formalizzarli attraverso un linguaggio adeguato.
La logica fa parte della nostra vita quotidiana ma nei linguaggi matematici e informatici che ne derivano si esprime senza ambiguità.
Dalla logica moderna sono nati i linguaggi della programmazione informatica: proposizioni, algoritmi e connettivi (operatori booleiani) sono le basi del coding.
NOTA
Charles Babbage viene considerato il padre dei computer moderni: a lui si deve infatti l'invenzione nel 1837 della prima “macchina analitica” che aveva dispositivi di ingresso basati su schede perforate, ma fu Ada Lovelace (Augusta Ada Byron) ad intuirne le reali possibilità e a produrre il primo algoritmo espressamente inteso per essere elaborato da una macchina.
Questo progetto rappresenta anche un piccolo tributo a tutte le donne in STEM.






.jpg)