Pre-requisiti:
- Conoscenza delle principali caratteristiche di un quadrato e della formula per calcolarne l'area.
- Conoscenza di base di Scratch (istruzioni sequenziali, cicliche, variabili).
Suddividete gli studenti in gruppi di lavoro, così da far lavorare 2-3 alunni su ogni computer.
Lavorate insieme a loro alla creazione un algoritmo con le seguenti caratteristiche:
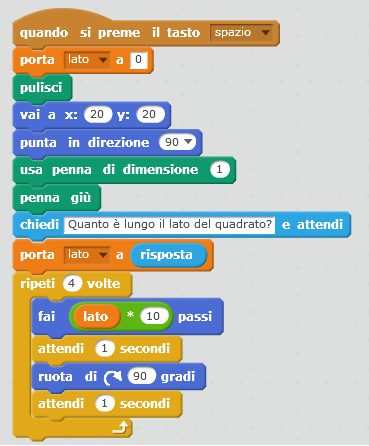
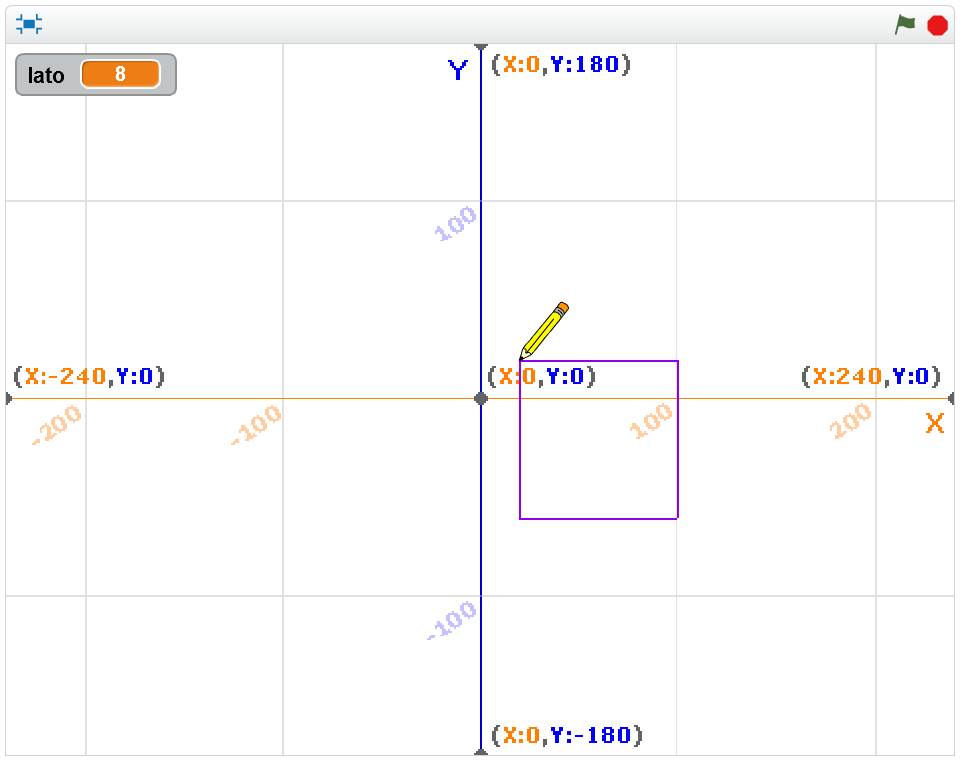
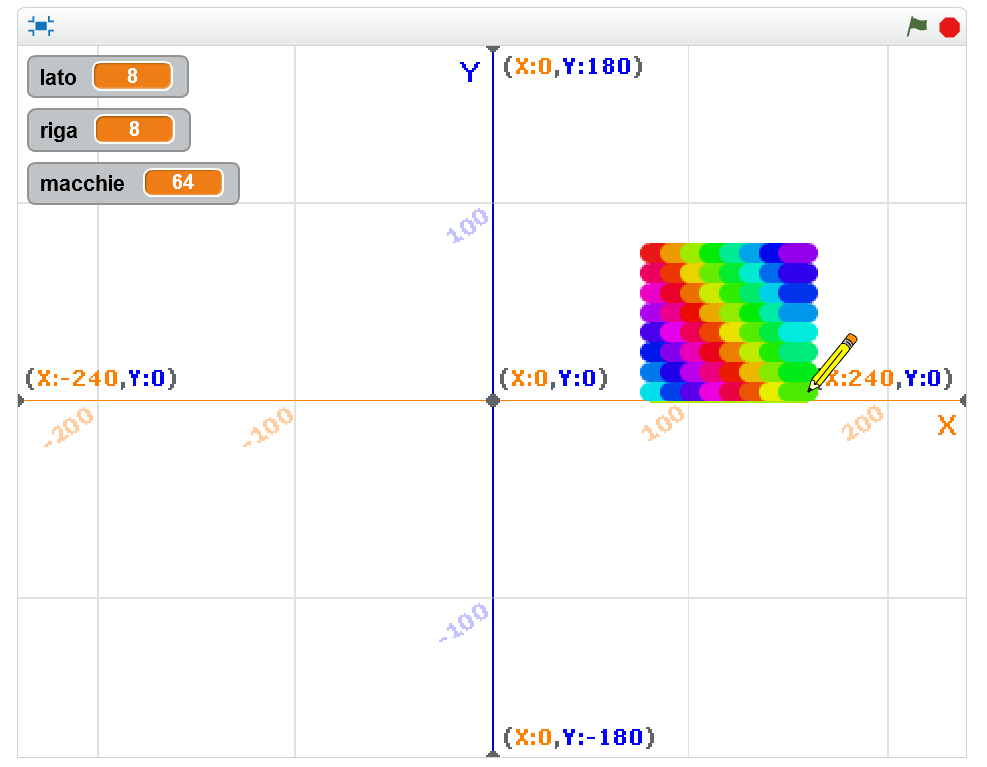
- il personaggio (nel nostro caso stiamo utilizzando lo sprite “pencil”, cioè la matita) dovrà chiedere all'utente quanto misura il lato del quadrato che si vuole disegnare. Attenzione: per rendere la figura facilmente visibile, è consigliabile scegliere una scala da applicare alla lunghezza del lato scelta dall’utente! Ad esempio nel nostro caso disegniamo il lato in scala 10:1 rispetto al all’unità di misura “passo” tipica di Scratch, così da visualizzare un lato lungo 80 passi nel caso in cui l’utente scelga un lato lungo 8.
- dopo la risposta dell'utente, la matita inizierà a muoversi disegnando il perimetro del quadrato con le dimensioni scelte.
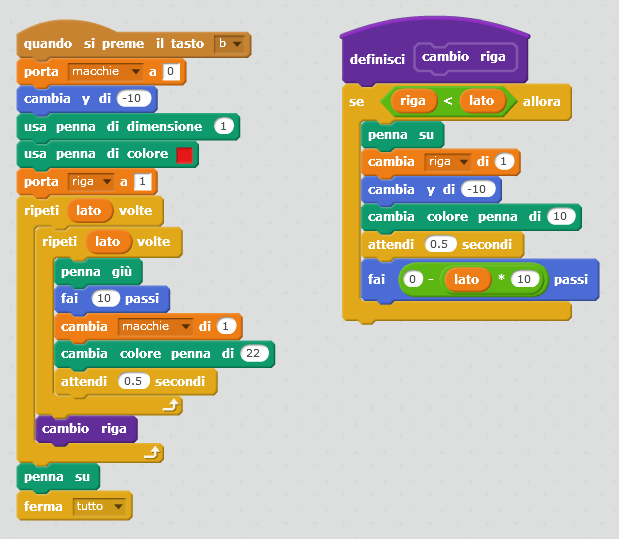
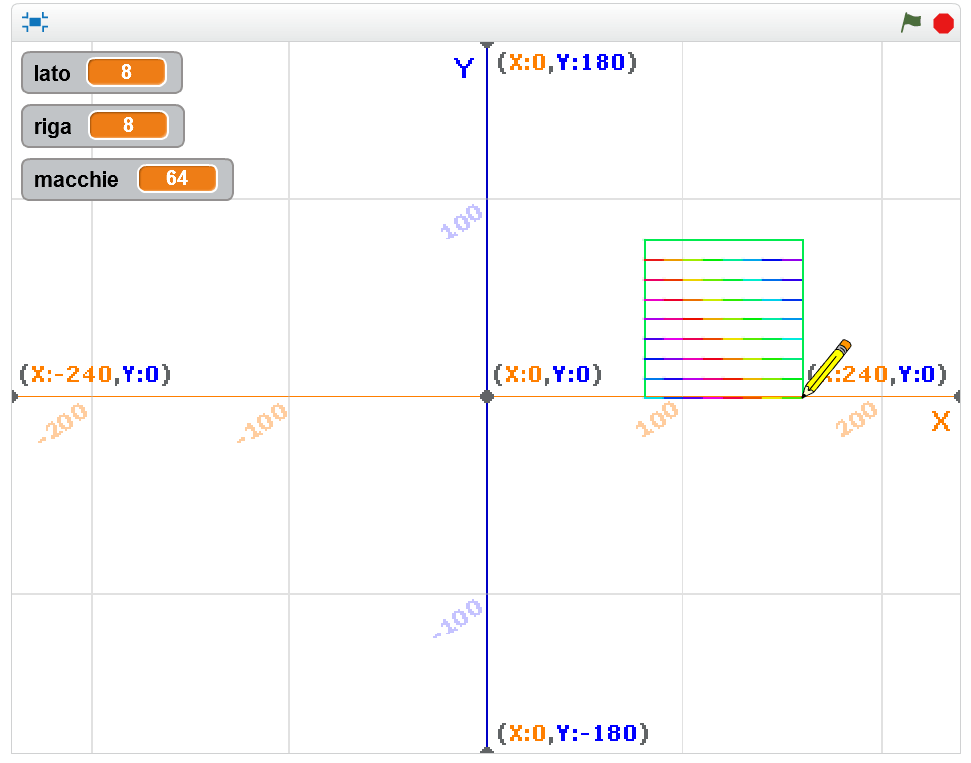
Una possibile soluzione potrebbe essere quella seguente: la variabile “lato” viene inizializzata a 0 (blocco “porta lato a 0” della categoria Variabili), ogni disegno precedentemente realizzato viene cancellato grazie al blocco “pulisci” (categoria Penna), la matita viene posizionata in una posizione determinata (nel nostro caso X=20, Y=20, orientamento 90° rispetto all’asse Y), viene scelta la dimensione della penna (blocco “usa penna di dimensione 1”, categoria Penna), viene appoggiata la penna sullo sfondo (blocco “penna giù”, categoria Penna) e a questo punto si chiede all’utente quanto è lungo il lato del quadrato (blocco “chiedi …. E attendi”, della categoria Sensori).
La risposta dell’utente (blocco “risposta”, categoria Sensori), viene utilizzato come input per la nuova assegnazione di valore alla variabile “lato” (“porta lato a risposta”).
Possiamo infine dare il via al movimento del nostro personaggio, disegnando i 4 lati di lunghezza lato*10 (scala 10:1) con il blocco “fai … passi” (categoria Movimento), pausa di un secondo, rotazione di 90 gradi in senso orario (categoria Movimento), pausa di un secondo. Questi ultimi 4 blocchi vanno inseriti all’interno di un “ripeti 4 volte” (categoria Controllo), così da ottenere i 4 lati del quadrato desiderato. La pausa di un secondo è stata inserita per poter visualizzare “step-by-step” la costruzione del perimetro del quadrato.